Winkelfunktionen

Sinus-Funktion
(c) Friedrich Sick
sinus-1
Wenn man sich mit Wechselstromtechnik befassen will, sollte man unbedingt über die Winkelfunktionen informiert sein. Eine davon ist die

  • Sinus-Funktion

    Der Sinuswert ist nichts weiter als die horizontale Projektion (Schattenlänge) eines rotierenden Zeigers mit der Länge 1 bei einer bestimmten Winkelstellung. (Bild 1)
    Während einer Umdrehung des sog. Einheitszeigers steigt der Sinuswert von 0 (bei 0° - Stellung) bis zum Wert 1 (bei 90°-Stellung). Fällt dann wieder ab bis zum Wert 0 (bei 180°-Stellung) um dann bei der 270°-Stellung des Zeigers das negative Maximum von -1 zu erreichen. Bei 360° ist der Sinuswert wieder 0!
    Jeder Winkelstellung des Zeigers lässt sich also eine bestimmte Projektions- bzw. Schattenlänge zuordnen. Überträgt man diese Werte in eine Grafik, so erhält man die sog. Sinus-Kurve*) (Siehe Bild 1 rechts!)

    *)Sinus = griech. Busen

  • Bild 1

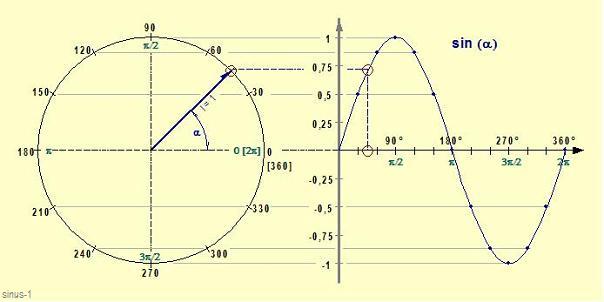
    Aus der Winkelstellung des Einheitszeigers im Einheitskreis lässt sich auf den Sinuswert schließen. Z.B.:
    sin (45°) = 0,707 (sprich: Sinus von 45° ist 0,707)! Aber auch umgekehrt vom Sinuswert auf die Winkelstellung des Zeigers - hier allerdings nicht eindeutig: Z.B. entspricht
    sin 0,5 = 30° / 150° ! (sprich: sin 0,5 entspricht 30° und 150°)
  • An Stelle des Winkels wird häufig auch mit dem Radianten (Bogenmaß) gerechnet. Es ist die Umfangsstrecke die der Einheitszeiger bei einer bestimmten Winkelstellung zurückgelegt hat. Berechnung:
    rad (a) = 2pa/360
    Beispiel: Bestimmung des Bogenmaßes für den Winkel von 90°
    rad (90°) = 2p* 90° / 360° = p/2 = 1,571 (siehe Bild 1 - Kreisdiagramm links!)
  • Die Zuordnung von Winkelstellung oder Radiant zum Sin-Wert sind in technischen Taschenrechnern gespeichert. Soll mit dem Radiant gerechnet werden, so muss der Rechner von DEG auf RAD umgestellt werden!